Poker With Buddies: Online Texas Hold Em Poker With Friends
Play ad-free fixed limit Texas Hold’Em poker online against friends, family, strangers, or strange family members. 😀
- Enter your desired screen name.
- Click on quick play to join a game with strangers.
- Click on private room to start a table of your own or join a game a friend created & share the room password with other friends to play against them.
- Bid smart & play to win. Strategy tips are published under the game.
Play Poker With Buddies Game Online
Children and parents can play this multiplayer online card game with friends by clicking in the window below.

Alternatively kids and adults can play this cards game for free as a web application .
Online Poker With Friends Game Play Instructions
How to Play
Play poker online against strangers or in a room where you invite friends to play.
- Starting the Game
- Select your icon from the 10 options.
- Enter your name.
- Choose the game type you like:
- Select “quick play” if you want to play against strangers.
- Select “private game” if you want to play against friends. Enter the password for the room if a friend created it, or if you are creating a new room make up the password and share the password with friends you want to play against.
- Playing against friends is much more fun than playing against strangers as you gain bragging rights & strangers can bet irrationally, stand up, and re-enter public tables with new usernames repeatedly.
- Game Controls
- Desktop
- Use your mouse left click button to fold, check, or raise.
- Mobile
- Use your finger like a mouse.
- There is a menu gear button in the upper right corner of the game.
- Players can click on it to adjust sound or music settings & read the game rules.
- There is a game log and chat box in the lower left corner of the game.
- Desktop
- Game Play
- Stakes & Pot
- Players start the game with $10,000 in chips.
- The small blind is $50 and the big blind is $100.
- The pot amount is shown in the upper left corner.
- You can raise $100 pre-flop or after the flop.
- You can raise $200 after the turn & river.
- Cumulatively players can raise a maximum of 4 times per round (meaning a maximum total cumulative raise of $400 for the first 2 rounds & $800 for the last 2 rounds of betting).
- Table size
- Tables can contain 3 to 6 total players.
- All players are human.
- Moves
- Players are given 30 second to make their move each turn & there are 5 seconds between each game.
- If you do not move in time you default to checking at the end of 30 seconds.
- Stakes & Pot
- Target Audience
- This game is fun for all poker fans.
- The game uses poker chips which are free, and of course is technically a gambling game, but this game and page are add free.
Hand Probabilities
Starting Odds for Hold Cards
- 5.8% (or 1 in 17) of hands will be dealt a pair
- 23.5% of hands will start off suited
- 70.6% of hands will start off offsuit
Breaking things down more specifically…
- 1 in 331 hands will be dealt same suit ace-king
- 1 in 221 hands will be dealt pocket aces
- 1 in 81 hands will be dealt out of suit ace-king
- 1 in 41 hands will be dealt a top 5 pair (e.g. pairs of tens or better)
- 1 in 5 hands will be dealt connecting cards
7 Card Poker Probabilities
The following table highlights the random odds of any hand type in a 7-card poker game.
| Poker Hand | Frequency | Probability | Cumulative | Odds against |
|---|---|---|---|---|
| Royal flush | 4,324 | 0.0032% | 0.0032% | 30,939 : 1 |
| Straight flush (excluding royal flush) | 37,260 | 0.0279% | 0.0311% | 3,589.6 : 1 |
| Four of a kind | 224,848 | 0.168% | 0.199% | 594 : 1 |
| Full house | 3,473,184 | 2.60% | 2.80% | 35.7 : 1 |
| Flush (excluding royal flush and straight flush) | 4,047,644 | 3.03% | 5.82% | 32.1 : 1 |
| Straight (excluding royal flush and straight flush) | 6,180,020 | 4.62% | 10.4% | 20.6 : 1 |
| Three of a kind | 6,461,620 | 4.83% | 15.3% | 19.7 : 1 |
| Two pair | 31,433,400 | 23.5% | 38.8% | 3.26 : 1 |
| One pair | 58,627,800 | 43.8% | 82.6% | 1.28 : 1 |
| No pair / High card | 23,294,460 | 17.4% | 100% | 4.74 : 1 |
| Total | 133,784,560 | 100% | — | 0 : 1 |
Since players share cards on in Texas Holdem the odds of certain hand combinations are higher. For example, if the table is showing 3 8s then there is a higher chance of a competitor having 4 of a kind or a full house than whatever the random odds would be since they too have that 3 of a kind in their hand. The odds of two players both having a straight or flush would be elevated as well if many of the key cards that make up the combination are on the table.
Shorthand Ranking Systems for Playable Texas Hold’em Hands
Hand rankings have a lot of value for limit play, however in no limit play their value deteriorates quickly as the downside of “all in” is an exit from the game. Here are some notable ranking systems.
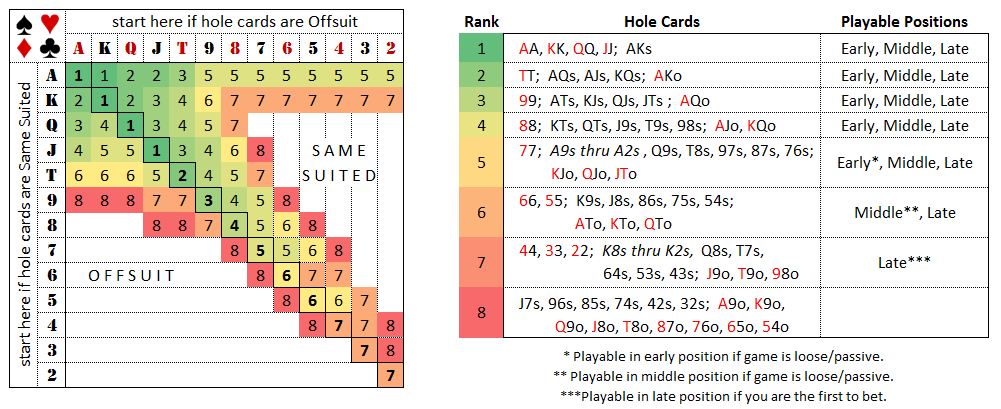
Sklansky Hand Groups
David Sklansky and Mason Malmuth created a diagram suggesting when hands should be played, with stronger hands having a lower number.
Phil Hellmuth
Similarly, Phil Hellmuth’s 2003 book Play Poker Like the Pros grouped hands by tiers.
| Tier | Hands | Category |
|---|---|---|
| 1 | AA, KK, AKs, QQ, AK | Top 12 Hands |
| 2 | JJ, TT, 99 | Top 12 Hands |
| 3 | 88, 77, AQs, AQ | Top 12 Hands |
| 4 | 66, 55, 44, 33, 22, AJs, ATs, A9s, A8s | Majority Play Hands |
| 5 | A7s, A6s, A5s, A4s, A3s, A2s, KQs, KQ | Majority Play Hands |
| 6 | QJs, JTs, T9s, 98s, 87s, 76s, 65s | Suited Connectors |
Chen Formula
Bill Chen developed what he called the “Chen Formula” which assigns points as follows
High Card
- Ace = 10
- King = 8
- Queen = 7
- Jack = 6
- 10 = 5
- 9 = 4.5
- 8 = 4
- 7 = 3.5
- 6 = 3
- 5 = 2.5
- 4 = 2
- 3 = 1.5
- 2 = 1
Pairs
Multiply the points by 2. A pair of aces would be worth 20, a pair of kings would be worth 16, and the minimum value for a pair is 5.
Suited
If cards are of the same suit add 2 points as you are more likely to be able to get a flush.
Closeness
This is given weight based on the probability you may be able to get a straight.
- Add an extra point if your cards are connected or a 1-gap and your highest card is below a queen.
- Subtract a point if there is a number between your cards (e.g. the king is between an ace and a queen).
- Subtract 2 points if there are 2 numbers between your cards.
- Subtract 4 points if there are 3 numbers between your cards.
- Subtract 5 points if there are more than 3 numbers between your cards (as you won’t be able to use both of your cards as part of a straight).
After the flop you then have to shift your approach based on the cards on the table.
Hand Strength and Tie Breakers
The strength of hands is as follows:
- Royal Flush
- Straight Flush
- Four of a Kind
- Full House
- Flush
- Straight
- Three of a Kind
- Two Pair
- Pair
- High Card
The approximate odds of various hands was shown above in the 7-card poker section, though the odds of rarer hands could technically be experienced more commonly in texas hold’em (particularly limit play) as players are not committed to throw away cards in order to see additional cards. A player could make a straight or a flush on the final card when they may not have played those cards in a 7-card game where they were forced to throw away a pair in order to make a flush or straight. Here are the odds using a 7 out of 52 hand where you get to make your 5 cards from a group of 7 you hold.
| Hand | Example Cards | Possibile Combos | Probability | Odds |
|---|---|---|---|---|
| Royal Flush |  |
4,324 | 0.003232062% | 30,939:1 |
| Straight Flush |  |
37,260 | 0.027850748% | 3,589.57:1 |
| Four-of-a-kind |  |
224,848 | 0.168067227% | 594:1 |
| Full House |  |
3,473,184 | 2.596102271% | 37.52:1 |
| Flush |  |
4,047,644 | 3.025494123% | 32.05:1 |
| Straight |  |
6,180,020 | 4.619382087% | 20.65:1 |
| Three-of-a-kind |  |
6,461,620 | 4.829869755% | 19.7:1 |
| Two pair |  |
31,433,400 | 23.49553641% | 3.26:1 |
| Pair |  |
58,627,800 | 43.82254574% | 1.28:1 |
| High card |  |
23,294,460 | 17.41191958% | 4.74:1 |
If two players have the exact same hand then the pot is split. If both hands are quite similar then the card value of the most important piece determines the winner. For example, if 2 players have a full house then whoever has the higher 3 of a kind wins. And if the 3 of a kind is the same for both players then whoever has the highest pair wins. For flushes or straights whoever has the highest card as part of that sequence wins. For games where both players have the same 4 of a kind, 3 of a kind, pair, etc. … then the remaining high card the player hold determines who wins.
The Flop
Many great hands are made on the flop between the cards in player’s hands and the cards on the flop. The flop by itself typically does not have much in the way of playable cards in absolute isolation. Typically the flop by itself (without the cards in player’s hands) is rather pedestrian. On the flop most the time cards are not connected, no pairs are shown, and there are rarely more than 2 cards in the same suit.
| Flop Cards | Probability | Odds |
|---|---|---|
| Three-of-a-kind | 0.24% | 415.67:1 |
| Pair | 16.9% | 4.91:1 |
| 3 suited cards | 5.17% | 18.34:1 |
| 2 suited cards | 55% | 0.82:1 |
| Rainbow | 39.8% | 1.5:1 |
| 3 connected straight cards | 3.45% | 27.99:1 |
| 2 connected straight cards | 40% | 1.5:1 |
| No connected cards | 55.6% | 0.799:1 |
The following table shows your probability of various hand improvements on the flop given a specific set of pocket cards.
| Pocket hand | Flop Improvement | Probability | Odds |
|---|---|---|---|
| Pair | Three-of-a-kind or better | 12.7% | 6.9:1 |
| Pair | Three-of-a-kind | 11.8% | 7.5:1 |
| Pair | Full house | 0.73% | 136:1 |
| Pair | Four-of-a-kind | 0.24% | 415.67:1 |
| 2 unpaired cards | Pair | 32.4% | 2.1:1 |
| 2 unpaired cards | Two pair | 2% | 48.5:1 |
| Suited cards | Flush | 0.842% | 118:1 |
| Suited cards | Flush draw | 10.9% | 8.17:1 |
| Suited cards | Backdoor flush draw | 41.6% | 1.4:1 |
| Connectors 45o-JTo | open ended straight draw | 9.6% | 9.42:1 |
| Connectors 45s-JTs | Straight draw / flush draw |
19.1% | 4.21:1 |
| Connectors 45o-JTo | Straight | 1.31% | 75:1 |
The Turn
After the flop comes the turn. The following table shows the odds of upgrading your hand on the turn.
| Current Hand | Turn Goal | Probability | Odds |
|---|---|---|---|
| Flush draw | Flush | 19.1% | 4.24:1 |
| Open ended straight draw | Straight | 17% | 4.9:1 |
| Gutshot straight draw | Straight | 8.5% | 10.76:1 |
| Three-of-a-kind | Four-of-a-kind | 2.1% | 46.61:1 |
| Two pair |
Full house | 8.5% | 10.76:1 |
| Pair | Three-of-a-kind | 4.3% | 22.26:1 |
| Two unpaired cards | Pair with a hole card | 12.8% | 6.8:1 |
The River
After the turn comes the river. The following table shows the odds of upgrading your hand on the river.
| Current Hand | River Goal | Probability | Odds |
|---|---|---|---|
| Flush draw | Flush | 19.6% | 4.1:1 |
| Open ended straight draw | Straight | 17.4% | 4.74:1 |
| Gutshot straight draw | Straight | 8.7% | 10.5:1 |
| Three-of-a-kind | Four-of-a-kind | 2.2% | 45.46:1 |
| Two pair |
Full house | 8.7% | 10.5:1 |
| Pair | Three-of-a-kind | 4.3% | 22.26:1 |
| Unpaired cards | Pair with hole card | 13% | 6.7:1 |
Understanding Outs
Each Texas Holdem hand has an “ideal” or best outcome available to it based on how things look after the flop.
After you have seen the flop and the cards in your hand you may need 1 card to complete a flush, a straight, a full house, a 3 of a kind, etc.
What you do is figure out how many cards from the deck remain and how many would satisfy your best hand.
For example, if you have 2 clubs in your hand and 2 clubs are showing on the table that means 4 of the 13 clubs are already gone, so there are 9 remaining clubs.
Each deck has 52 cards. You know what the 3 cards on the flop were as well as the 2 in your hand, so if you subtract those 5 cards that means there are 47 left. On the turn you would have a 9 in 47 (or 19.1%) chance of getting another club. If that card was not a club you would have a 9 in 46 (or 19.6%) chance on the river.
| Outs | Odds After Flop | Odds After Turn |
|---|---|---|
| 1 | 4.4% | 2.2% |
| 2 | 8.4% | 4.3% |
| 3 | 12.5% | 6.5% |
| 4 | 16.5% | 8.7% |
| 5 | 20.3% | 10.9% |
| 6 | 24.1% | 13% |
| 7 | 27.8% | 15.2% |
| 8 | 31.5% | 17.4% |
| 9 | 35% | 19.6% |
| 10 | 38.4% | 21.7% |
| 11 | 41.7% | 24% |
| 12 | 45% | 26.1% |
| 13 | 48.1% | 28.3% |
| 14 | 51.2% | 30.4% |
| 15 | 54.1% | 32.6% |
| 16 | 57% | 34.3% |
| 17 | 59.8% | 37% |
| 18 | 62.4% | 39.1% |
| 19 | 65% | 41.3% |
| 20 | 67.5% | 43.5% |
Combining Flop & River Odds
Below are the odds of completing common card scenarios on the turn, river, or across both.
| Hand | Outs | Flop to Turn | Turn to River | Turn + River | Odds |
|---|---|---|---|---|---|
| Pocket pair to 3 of a kind | 2 | 4.3% | 4.3% | 8.4% | 10.9:1 |
| Pair to 4 of a kind | 1* | – | – | 0.09% | 1,100:1 |
| Completing a pair of a high card | 3 | 6.4% | 6.5% | 12.5% | 7:1 |
| Completing a pair of either high card | 6 | 12.8% | 13.0% | 25% | 3:1 |
| Inside (gunshot) straight draw to straight | 4 | 8.5% | 8.7% | 16.5% | 4.88:1 |
| Two pair to full house | 4 | 8.5% | 8.7% | 16.5% | 4.88:1 |
| Two overcards to overpair | 6 | 12.8% | 13% | 24.1% | 3.15:1 |
| 3 of a kind to 4 of a kind | 1 | 2.1% | 2.2% | 4.3% | 22.26:1 |
| 3 of a kind to full house or 4 of a kind | 7 | 14.9% | 15.2% | 27.8% | 2.60:1 |
| Open ended straight draw to straight | 8 | 17% | 17.4% | 31.5% | 2.13:1 |
| Flush draw to flush | 9 | 19.1% | 19.6% | 35% | 1.86:1 |
| Backdoor flush draw to flush | 1* | – | – | 4.2% | 22.8:1 |
| Inside straight and flush draw to straight or flush | 12 | 25.5% | 26.1% | 45% | 1.22:1 |
| Open ended straight and flush draw to straight or flush | 15 | 31.9% | 32.6% | 54.1% | 0.85:1 |
* Rather than there being multiple outs, you need 2 consecutive cards to go your way. Individual odds not shown for flop and turn since you need both to go your way.
Understanding Pot Odds
When deciding if it makes sense to play you not only have to consider the odds of victory, but also the size of the pre-existing pot and the amount your competitor bet. If the raise was small relative to the pot size then you have to factor in the larger potential upside of winning the larger pot against the downside of the smaller incremental raise.
- Betting on 1 in 3 Odds: For example, if a pot is $200 and another player raises $20 and you have a 1 in 3 chance of hitting your out then it makes sense to bet as your upside is 10x the side of the bet and you have a 1 in 3 chance of hitting it.
- Not Betting on 1 in 3 Odds: Flipping things around, if the pot size was $200 and another player raised $300 then the 1 in 3 chances of hitting your out are less appealing since your upside would be less than you were wagering and your odds of hitting are below 50%.
The above is purely mathematical in terms of considering probability on a particular bet. There are also human emotions, bluffing, re-raising a raise, and many other factors to consider which makes poker a complex game beyond the math aspect of pot odds.
Winning at poker is not only figuring your odds of hitting what you want, but also if an opponent have almost the same hand with a higher kicker or if the shared cards which enabled your great hand enabled some other better hand for them.
Where & When Are the Key Cards Located?
If you are holding 2 pocket spades and you get a flush on the turn or river and there are only a total of 3 spades showing on the table the odds of someone else having a spades flush are low.
If, however 4 spades are on the table and many players are still in the game it is likely one of the competing players also has a flush, so in that case it matters what spade you have in your hand. If you have a 2 or a 4 and they have a facecard you will lose.
Most players may bail on a potential flush if they only have 1 card in their hand, get 2 on the flop and need both the turn and river to be of that same suit. If, however, the flop itself has 3 of the same suit there are likely to be other players holding a spade who stayed in the game hoping on a fifth spade.
The above sort of thinking is also true with a straight. If you have an outside straight and your card is to the low side there is a good chance a competing player has an outside straight with a higher top card than you do.
The same sort of thinking is true if you flop a 3 of a kind where 2 of the pair are on the flop. Someone else playing may have the 4th of that card & they might also have a higher high card than you do or a full house with a higher second card. If you flop a 3 of a kind with all 3 being on the flop there is a good chance someone else will have a 4 of a kind or a full house with another pair.
Like This Game? Review This Online Card Playing Video Game
Free Online Poker With Buddies Game Screenshots


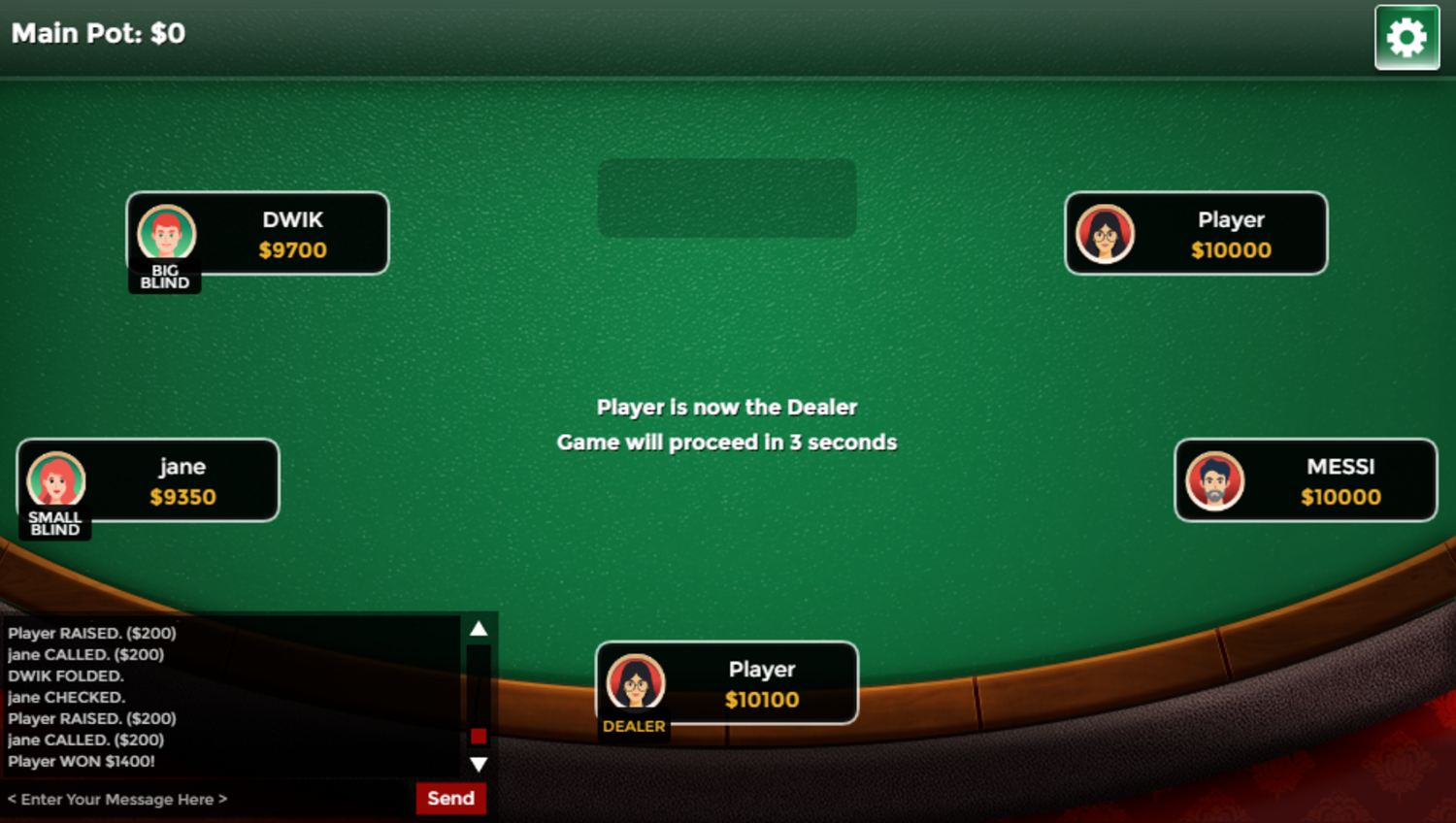
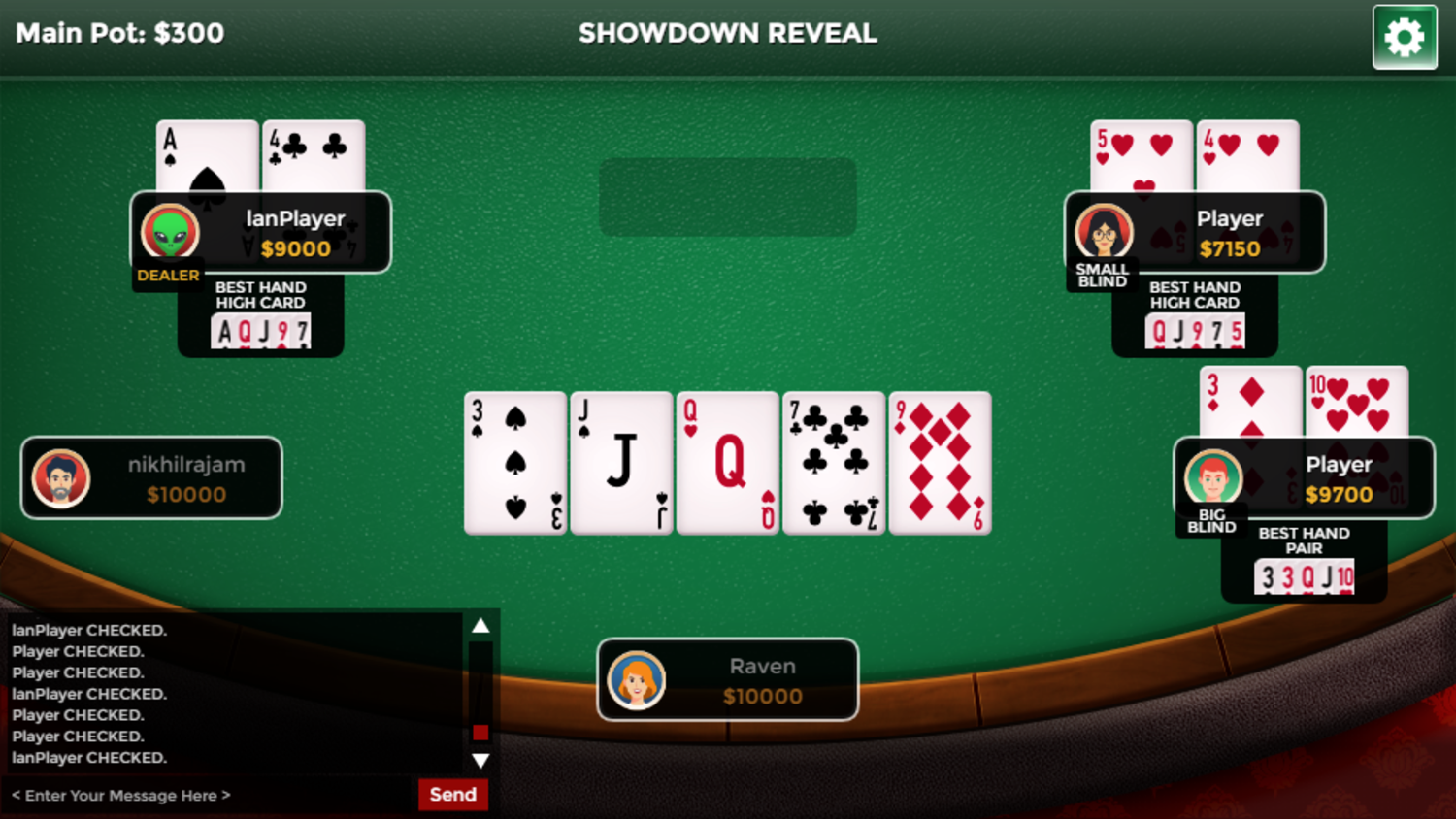
Mobile Friendly Cross Browser Support
This game is rendered in mobile-friendly HTML5, so it offers cross-device gameplay. You can play it on mobile devices like Apple iPhones, Google Android powered cell phones from manufactures like Samsung, tablets like the iPad or Kindle Fire, laptops, and Windows-powered desktop computers. All game files are stored locally in your web browser cache. This game works in Apple Safari, Google Chrome, Microsoft Edge, Mozilla Firefox, Opera and other modern web browsers.
Where To? What Next?
This game was published in these categories: 2 Player, Poker. You can visit any of them to select other fun games to play.
Our site hosts thousands of free online games. Check out the newest additions to our library or play a random game!
This game was published using our teamwide CardGames.pro account. If you have any comments, questions, concerns, or others (are there others even???) you can use the comments below to send along your 2 cents and help us improve the site further :) Your 2 cents plus 3 cents will buy you a nickel, but if your comments are genuinely useful and/or helpful and/or funny and/or memorable in a good way, we will probably say thanks :D
Search And Find And CardGames.pro Your Free Online Games :)










