Banana Poker: Free Online Texas Hold’em Poker Video Game
Banana Poker is a cute and whimsical poker video game where players can choose to play either high / low card or Texas Holdem Poker against 5 other computer players. While we do not promote gambling with real money, this game can be useful for helping to teaching mathematical concepts like odds and probability along with the importance of exercising patience.
- Click on either the play now button to play Texas Holdem poker or the click on the high or low button.
- The high or low game asks you to guess the sequence of cards in a suit and rewards you with chips if you get enough of them correct without getting too many incorrect.
- The play now button starts a standard Texas Holdem game against the computer with 5 other computer players at the table.
- The game plays like a standard Texas Holdem game with small and big blinds, calls, and raises.
Play Banana Poker Video Game Online
Children and parents can play this cartoon card card game by clicking in the window below.

Alternatively kids and adults can play this virtual texas holdem cartoon card game for free as a web application .
Banana Poker Texas Holdem Card Game Play Instructions
How to Play Spider Solitaire
Bet on hands you think you will win while folding on hands you think you are likely to lose.
- Starting the Game
- The welcome screen contains 5 different buttons on it.
- The + button in the upper left corner and the “High or Low” button start a game of high / low where you can earn up to 1,200 chips.
- The upper right corner of the welcome screen has a sound control button.
- The lower left corner has a player information button which shows the attributes of the 7 potential computer players you may play Texas Holdem Poker against. Each player profile contains an overall rating along with analysis, agressiveness, and volatility.
- The “Play Now” button starts a game of Texas Holdem Poker against 5 competing computer players chosen at random.
- The welcome screen contains 5 different buttons on it.
Playing High Low
High low is a much easier and less complex game than poker, so it makes sense to explain it first.
- The computer picks a suit and then throws out a card from that suit.
- You have to guess if the next card will be higher or lower.
- Cards are valued in the following order: 2, 3, 4, 5, 6, 7, 8, 9, 10. jack, queen, king, ace.
- Underneath the cards yet dealt it will show how many of the cards remain.
- This process continues until you get 3 wrong or the entire suit has been dealt.
- Each card you get right is worth 100 points.
- Each card you get wrong is worth -100 points.
- Each card you get wrong also takes 1 of your 3 hearts.
- You can earn extra hearts by getting 5 in a row correct.
- If you lose you do not lose any chips, but if you win the chips are added to your stack.
- Tips
- Understand Range Limits
- If a 2 is dealt you know the next card will be higher.
- If an ace is dealt you know the next card will be lower.
- Track Cards Already Laid
- Each card can only be thrown once, so you can track which cards have been thrown to know the approximate odds of the next card being higher or lower.
- If the ace and king have already been dealt and you are shown a jack then the only higher card left would be a queen, meaning that if there are more than a couple cards left the odds are the next card will be lower.
- If you know there are 9 cards remaining and only 3 of them are lower than the card shown on the board then there is a 6 in 9 or 2 in 3 chance the next card will be higher.
- Understand Range Limits
Playing No Limit Texas Holdem Poker
How To Play
- Click start to start the game. The goal of the game is to be the last person at the poker table with chips left. All players start with 1,000 chips.
- Dealing
- When you begin a game of Texas Holdem you are dealt 2 cards that only you can see & the other players are also dealt two cards.
- You can bet after seeing your first 2 cards & you can bet after each subsequent deal.
- Players are dealt 5 cards on the table that are shared cards which can be used in all player hands.
- First there is the flop, where 3 cards are shared.
- Next there is the turn, where another card is shared.
- Finally there is the river card.
- Players can use any 5 cards from the combination of the 2 in their hand and the 5 which are on the table.
- When you begin a game of Texas Holdem you are dealt 2 cards that only you can see & the other players are also dealt two cards.
Blinds & Betting
- Dealing Basics
- If you do not like your cards you can fold. If you like your cards you can call the baseline bet of 10, or raise the pot to a higher amount.
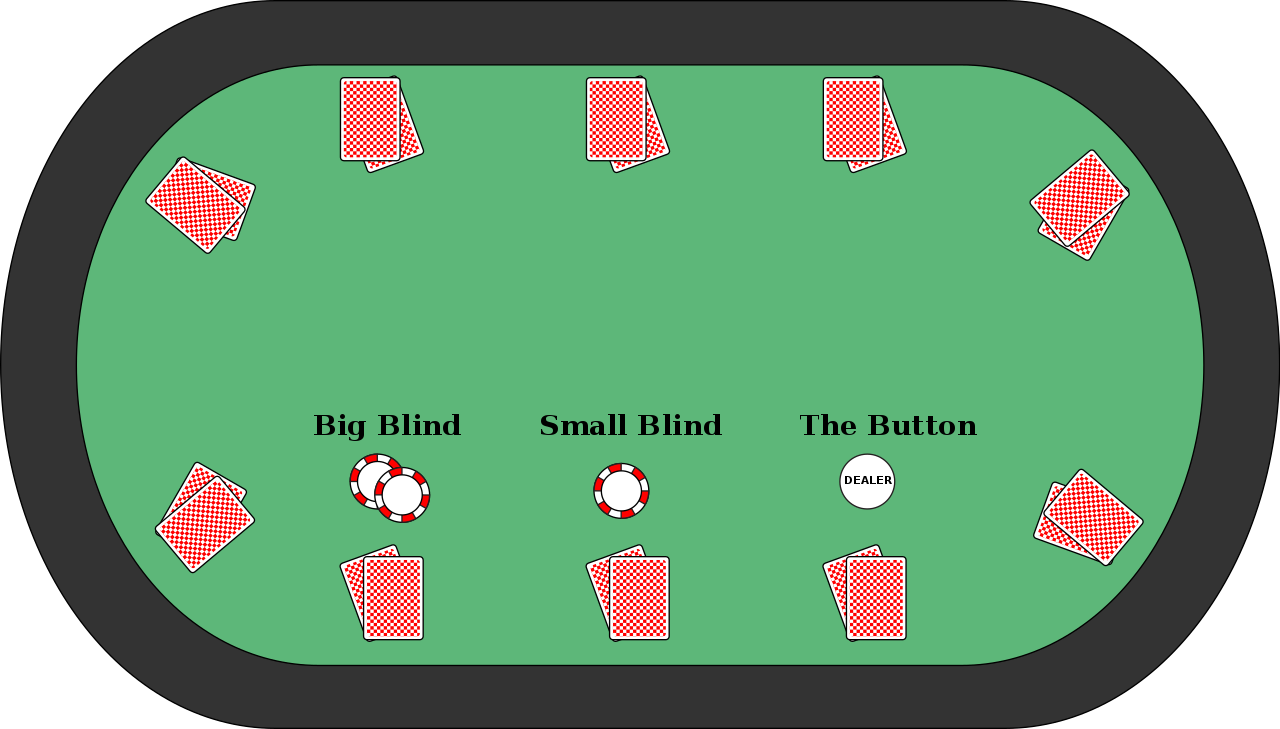
- When a poker dealer deals a Texas Hold’em game there is a button they move around the table. The player one spot in front of the button is the small blind and the player in front of them is the big blind.
- The reason for the small blind and big blind is to ensure people have an incentive to bid and play rather than folding hand after hand until they get great cards.
- The blind players are forced to bid before they see their cards no matter what.
- This game starts off with a 5 chip small blind and a 10 chip big blind.
- After 9 hands the blind goes to 10 and 20 chips. It increases sequentially from there.
- Other players get to bet before the small and big blinds get a chance to bet.
- Folding
- If you think you have a low probability of winning you can fold at any point in the hand.
- If you fold you can click on the skip button to skip watching the hand & speed up play.
- Check
- Checking or calling means you agree to bet the default amount for the round or the amount dealt by prior players.
- Checking in the first round costs the same number of chips as the big blind, unless someone raises it.
- If nobody raises in a round after the first one then calling does not commit any more tips in that round.
- Checking or calling means you agree to bet the default amount for the round or the amount dealt by prior players.
- Raising
- If you think you have a strong chance of winning you can raise. Click the plus or minus signs near the edge of the slider to adjust your raise amount, or move the slider piece directly, then click on the bet button.
- When playing in person some players skip raising in order to try to get other players to raise & then re-raise them over the top.
- Such activity depends on knowing the psychology of the players.
- Scoring
- In each poker hand typically only 1 player wins. The sum total amount bet by all players is called the pot. The winner wins it at the end of the hand.
- If there are two players with the exact same hand they may tie & then split the pot in half.
- If you fold you are guaranteed to lose, though you limit how much you can lose if you fold early.
- If you check and nobody has raised you get a free look at the next card. If someone else raised and then you check it costs you more to see the next round.
- If you have great cards you can go beyond checking and raise the pot.
- At the end of the hand the winning player wins the pot.
- The game continues until all players but 1 have been eliminated from the poker table. Since there are 6 players with 1,000 chips each that means the winner will leave the table with 5,000 extra chips.
- In each poker hand typically only 1 player wins. The sum total amount bet by all players is called the pot. The winner wins it at the end of the hand.
- Strategy
- The player attributes for competing players in this game are shown in a table below.
- Against players who are more aggressive and less skilled you may want to bet more aggressively.
- Against players who are less aggressive and more analytical it may make sense to bet more conservatively (as they may only stay in hands with big hots if they believe they have a high probability of winning).
- Playing online poker is nothing like playing offline poker.
- You can play this game from anywhere & at any point in time you can pause or take a break.
- Without seeing people face to face you can not read their nonverbal communications.
- A large part of in-person poker is reading the ticks or tells of other players.
- This game plays with chips of no consequences & if a player loses they can stand up then sit down and play once again, losing nothing but a few seconds of their time.
- Players may find they are less comfortable playing for real money with real consequences.
- The point of these cautions is that many people who think they are great playing against a program get their butts handed to them when they play against professionals for real money.
- Many people ruin their lives with gambling from the stress it causes, ruining relationships by hiding losses & compounding them, etc.
- The player attributes for competing players in this game are shown in a table below.
Competing Player Profiles
The following table highlights how the competing players were programmed to play.
| Player | Overall | Analysis | Agressiveness | Volatility |
|---|---|---|---|---|
| Albertstein | 9 | 10 | 4 | 2 |
| Moaichel | 7 | 7 | 1 | 0 |
| Sloth Marley | 6.5 | 3 | 1 | 0 |
| Biff McNoob | 6 | 6 | 5 | 0 |
| Lilith S. | 5 | 5 | 8 | 0 |
| Chimp Manson | 4 | 6 | 9 | 10 |
| Monsieur Bling | 2 | 4 | 7 | 0 |
Hand Probabilities
Starting Odds for Hold Cards
- 5.8% (or 1 in 17) of hands will be dealt a pair
- 23.5% of hands will start off suited
- 70.6% of hands will start off offsuit
Breaking things down more specifically…
- 1 in 331 hands will be dealt same suit ace-king
- 1 in 221 hands will be dealt pocket aces
- 1 in 81 hands will be dealt out of suit ace-king
- 1 in 41 hands will be dealt a top 5 pair (e.g. pairs of tens or better)
- 1 in 5 hands will be dealt connecting cards
7 Card Poker Probabilities
The following table highlights the random odds of any hand type in a 7-card poker game.
| Poker Hand | Frequency | Probability | Cumulative | Odds against |
|---|---|---|---|---|
| Royal flush | 4,324 | 0.0032% | 0.0032% | 30,939 : 1 |
| Straight flush (excluding royal flush) | 37,260 | 0.0279% | 0.0311% | 3,589.6 : 1 |
| Four of a kind | 224,848 | 0.168% | 0.199% | 594 : 1 |
| Full house | 3,473,184 | 2.60% | 2.80% | 35.7 : 1 |
| Flush (excluding royal flush and straight flush) | 4,047,644 | 3.03% | 5.82% | 32.1 : 1 |
| Straight (excluding royal flush and straight flush) | 6,180,020 | 4.62% | 10.4% | 20.6 : 1 |
| Three of a kind | 6,461,620 | 4.83% | 15.3% | 19.7 : 1 |
| Two pair | 31,433,400 | 23.5% | 38.8% | 3.26 : 1 |
| One pair | 58,627,800 | 43.8% | 82.6% | 1.28 : 1 |
| No pair / High card | 23,294,460 | 17.4% | 100% | 4.74 : 1 |
| Total | 133,784,560 | 100% | — | 0 : 1 |
Since players share cards on in Texas Holdem the odds of certain hand combinations are higher. For example, if the table is showing 3 8s then there is a higher chance of a competitor having 4 of a kind or a full house than whatever the random odds would be since they too have that 3 of a kind in their hand. The odds of two players both having a straight or flush would be elevated as well if many of the key cards that make up the combination are on the table.
Shorthand Ranking Systems for Playable Texas Hold’em Hands
Hand rankings have a lot of value for limit play, however in no limit play their value deteriorates quickly as the downside of “all in” is an exit from the game. Here are some notable ranking systems.
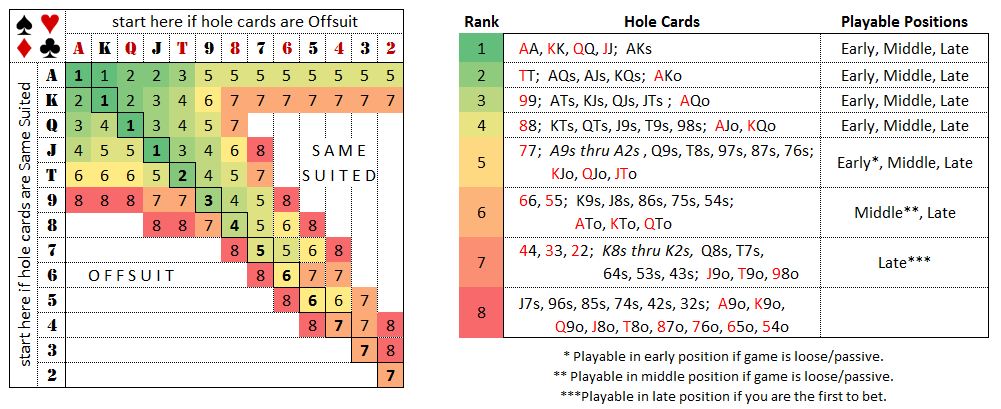
Sklansky Hand Groups
David Sklansky and Mason Malmuth created a diagram suggesting when hands should be played, with stronger hands having a lower number.
Phil Hellmuth
Similarly, Phil Hellmuth’s 2003 book Play Poker Like the Pros grouped hands by tiers.
| Tier | Hands | Category |
|---|---|---|
| 1 | AA, KK, AKs, QQ, AK | Top 12 Hands |
| 2 | JJ, TT, 99 | Top 12 Hands |
| 3 | 88, 77, AQs, AQ | Top 12 Hands |
| 4 | 66, 55, 44, 33, 22, AJs, ATs, A9s, A8s | Majority Play Hands |
| 5 | A7s, A6s, A5s, A4s, A3s, A2s, KQs, KQ | Majority Play Hands |
| 6 | QJs, JTs, T9s, 98s, 87s, 76s, 65s | Suited Connectors |
Chen Formula
Bill Chen developed what he called the “Chen Formula” which assigns points as follows
High Card
- Ace = 10
- King = 8
- Queen = 7
- Jack = 6
- 10 = 5
- 9 = 4.5
- 8 = 4
- 7 = 3.5
- 6 = 3
- 5 = 2.5
- 4 = 2
- 3 = 1.5
- 2 = 1
Pairs
Multiply the points by 2. A pair of aces would be worth 20, a pair of kings would be worth 16, and the minimum value for a pair is 5.
Suited
If cards are of the same suit add 2 points as you are more likely to be able to get a flush.
Closeness
This is given weight based on the probability you may be able to get a straight.
- Add an extra point if your cards are connected or a 1-gap and your highest card is below a queen.
- Subtract a point if there is a number between your cards (e.g. the king is between an ace and a queen).
- Subtract 2 points if there are 2 numbers between your cards.
- Subtract 4 points if there are 3 numbers between your cards.
- Subtract 5 points if there are more than 3 numbers between your cards (as you won’t be able to use both of your cards as part of a straight).
After the flop you then have to shift your approach based on the cards on the table.
Hand Strength and Tie Breakers
The strength of hands is as follows:
- Royal Flush
- Straight Flush
- Four of a Kind
- Full House
- Flush
- Straight
- Three of a Kind
- Two Pair
- Pair
- High Card
The approximate odds of various hands was shown above in the 7-card poker section, though the odds of rarer hands could technically be experienced more commonly in texas hold’em (particularly limit play) as players are not committed to throw away cards in order to see additional cards. A player could make a straight or a flush on the final card when they may not have played those cards in a 7-card game where they were forced to throw away a pair in order to make a flush or straight. Here are the odds using a 7 out of 52 hand where you get to make your 5 cards from a group of 7 you hold.
| Hand | Example Cards | Possibile Combos | Probability | Odds |
|---|---|---|---|---|
| Royal Flush |  |
4,324 | 0.003232062% | 30,939:1 |
| Straight Flush |  |
37,260 | 0.027850748% | 3,589.57:1 |
| Four-of-a-kind |  |
224,848 | 0.168067227% | 594:1 |
| Full House |  |
3,473,184 | 2.596102271% | 37.52:1 |
| Flush |  |
4,047,644 | 3.025494123% | 32.05:1 |
| Straight |  |
6,180,020 | 4.619382087% | 20.65:1 |
| Three-of-a-kind |  |
6,461,620 | 4.829869755% | 19.7:1 |
| Two pair |  |
31,433,400 | 23.49553641% | 3.26:1 |
| Pair |  |
58,627,800 | 43.82254574% | 1.28:1 |
| High card |  |
23,294,460 | 17.41191958% | 4.74:1 |
If two players have the exact same hand then the pot is split. If both hands are quite similar then the card value of the most important piece determines the winner. For example, if 2 players have a full house then whoever has the higher 3 of a kind wins. And if the 3 of a kind is the same for both players then whoever has the highest pair wins. For flushes or straights whoever has the highest card as part of that sequence wins. For games where both players have the same 4 of a kind, 3 of a kind, pair, etc. … then the remaining high card the player hold determines who wins.
The Flop
Many great hands are made on the flop between the cards in player’s hands and the cards on the flop. The flop by itself typically does not have much in the way of playable cards in absolute isolation. Typically the flop by itself (without the cards in player’s hands) is rather pedestrian. On the flop most the time cards are not connected, no pairs are shown, and there are rarely more than 2 cards in the same suit.
| Flop Cards | Probability | Odds |
|---|---|---|
| Three-of-a-kind | 0.24% | 415.67:1 |
| Pair | 16.9% | 4.91:1 |
| 3 suited cards | 5.17% | 18.34:1 |
| 2 suited cards | 55% | 0.82:1 |
| Rainbow | 39.8% | 1.5:1 |
| 3 connected straight cards | 3.45% | 27.99:1 |
| 2 connected straight cards | 40% | 1.5:1 |
| No connected cards | 55.6% | 0.799:1 |
The following table shows your probability of various hand improvements on the flop given a specific set of pocket cards.
| Pocket hand | Flop Improvement | Probability | Odds |
|---|---|---|---|
| Pair | Three-of-a-kind or better | 12.7% | 6.9:1 |
| Pair | Three-of-a-kind | 11.8% | 7.5:1 |
| Pair | Full house | 0.73% | 136:1 |
| Pair | Four-of-a-kind | 0.24% | 415.67:1 |
| 2 unpaired cards | Pair | 32.4% | 2.1:1 |
| 2 unpaired cards | Two pair | 2% | 48.5:1 |
| Suited cards | Flush | 0.842% | 118:1 |
| Suited cards | Flush draw | 10.9% | 8.17:1 |
| Suited cards | Backdoor flush draw | 41.6% | 1.4:1 |
| Connectors 45o-JTo | open ended straight draw | 9.6% | 9.42:1 |
| Connectors 45s-JTs | Straight draw / flush draw |
19.1% | 4.21:1 |
| Connectors 45o-JTo | Straight | 1.31% | 75:1 |
The Turn
After the flop comes the turn. The following table shows the odds of upgrading your hand on the turn.
| Current Hand | Turn Goal | Probability | Odds |
|---|---|---|---|
| Flush draw | Flush | 19.1% | 4.24:1 |
| Open ended straight draw | Straight | 17% | 4.9:1 |
| Gutshot straight draw | Straight | 8.5% | 10.76:1 |
| Three-of-a-kind | Four-of-a-kind | 2.1% | 46.61:1 |
| Two pair |
Full house | 8.5% | 10.76:1 |
| Pair | Three-of-a-kind | 4.3% | 22.26:1 |
| Two unpaired cards | Pair with a hole card | 12.8% | 6.8:1 |
The River
After the turn comes the river. The following table shows the odds of upgrading your hand on the river.
| Current Hand | River Goal | Probability | Odds |
|---|---|---|---|
| Flush draw | Flush | 19.6% | 4.1:1 |
| Open ended straight draw | Straight | 17.4% | 4.74:1 |
| Gutshot straight draw | Straight | 8.7% | 10.5:1 |
| Three-of-a-kind | Four-of-a-kind | 2.2% | 45.46:1 |
| Two pair |
Full house | 8.7% | 10.5:1 |
| Pair | Three-of-a-kind | 4.3% | 22.26:1 |
| Unpaired cards | Pair with hole card | 13% | 6.7:1 |
Understanding Outs
Each Texas Holdem hand has an “ideal” or best outcome available to it based on how things look after the flop.
After you have seen the flop and the cards in your hand you may need 1 card to complete a flush, a straight, a full house, a 3 of a kind, etc.
What you do is figure out how many cards from the deck remain and how many would satisfy your best hand.
For example, if you have 2 clubs in your hand and 2 clubs are showing on the table that means 4 of the 13 clubs are already gone, so there are 9 remaining clubs.
Each deck has 52 cards. You know what the 3 cards on the flop were as well as the 2 in your hand, so if you subtract those 5 cards that means there are 47 left. On the turn you would have a 9 in 47 (or 19.1%) chance of getting another club. If that card was not a club you would have a 9 in 46 (or 19.6%) chance on the river.
| Outs | Odds After Flop | Odds After Turn |
|---|---|---|
| 1 | 4.4% | 2.2% |
| 2 | 8.4% | 4.3% |
| 3 | 12.5% | 6.5% |
| 4 | 16.5% | 8.7% |
| 5 | 20.3% | 10.9% |
| 6 | 24.1% | 13% |
| 7 | 27.8% | 15.2% |
| 8 | 31.5% | 17.4% |
| 9 | 35% | 19.6% |
| 10 | 38.4% | 21.7% |
| 11 | 41.7% | 24% |
| 12 | 45% | 26.1% |
| 13 | 48.1% | 28.3% |
| 14 | 51.2% | 30.4% |
| 15 | 54.1% | 32.6% |
| 16 | 57% | 34.3% |
| 17 | 59.8% | 37% |
| 18 | 62.4% | 39.1% |
| 19 | 65% | 41.3% |
| 20 | 67.5% | 43.5% |
Combining Flop & River Odds
Below are the odds of completing common card scenarios on the turn, river, or across both.
| Hand | Outs | Flop to Turn | Turn to River | Turn + River | Odds |
|---|---|---|---|---|---|
| Pocket pair to 3 of a kind | 2 | 4.3% | 4.3% | 8.4% | 10.9:1 |
| Pair to 4 of a kind | 1* | – | – | 0.09% | 1,100:1 |
| Completing a pair of a high card | 3 | 6.4% | 6.5% | 12.5% | 7:1 |
| Completing a pair of either high card | 6 | 12.8% | 13.0% | 25% | 3:1 |
| Inside (gunshot) straight draw to straight | 4 | 8.5% | 8.7% | 16.5% | 4.88:1 |
| Two pair to full house | 4 | 8.5% | 8.7% | 16.5% | 4.88:1 |
| Two overcards to overpair | 6 | 12.8% | 13% | 24.1% | 3.15:1 |
| 3 of a kind to 4 of a kind | 1 | 2.1% | 2.2% | 4.3% | 22.26:1 |
| 3 of a kind to full house or 4 of a kind | 7 | 14.9% | 15.2% | 27.8% | 2.60:1 |
| Open ended straight draw to straight | 8 | 17% | 17.4% | 31.5% | 2.13:1 |
| Flush draw to flush | 9 | 19.1% | 19.6% | 35% | 1.86:1 |
| Backdoor flush draw to flush | 1* | – | – | 4.2% | 22.8:1 |
| Inside straight and flush draw to straight or flush | 12 | 25.5% | 26.1% | 45% | 1.22:1 |
| Open ended straight and flush draw to straight or flush | 15 | 31.9% | 32.6% | 54.1% | 0.85:1 |
* Rather than there being multiple outs, you need 2 consecutive cards to go your way. Individual odds not shown for flop and turn since you need both to go your way.
Understanding Pot Odds
When deciding if it makes sense to play you not only have to consider the odds of victory, but also the size of the pre-existing pot and the amount your competitor bet. If the raise was small relative to the pot size then you have to factor in the larger potential upside of winning the larger pot against the downside of the smaller incremental raise.
- Betting on 1 in 3 Odds: For example, if a pot is $200 and another player raises $20 and you have a 1 in 3 chance of hitting your out then it makes sense to bet as your upside is 10x the side of the bet and you have a 1 in 3 chance of hitting it.
- Not Betting on 1 in 3 Odds: Flipping things around, if the pot size was $200 and another player raised $300 then the 1 in 3 chances of hitting your out are less appealing since your upside would be less than you were wagering and your odds of hitting are below 50%.
The above is purely mathematical in terms of considering probability on a particular bet. There are also human emotions, bluffing, re-raising a raise, and many other factors to consider which makes poker a complex game beyond the math aspect of pot odds.
Winning at poker is not only figuring your odds of hitting what you want, but also if an opponent have almost the same hand with a higher kicker or if the shared cards which enabled your great hand enabled some other better hand for them.
Where & When Are the Key Cards Located?
If you are holding 2 pocket spades and you get a flush on the turn or river and there are only a total of 3 spades showing on the table the odds of someone else having a spades flush are low.
If, however 4 spades are on the table and many players are still in the game it is likely one of the competing players also has a flush, so in that case it matters what spade you have in your hand. If you have a 2 or a 4 and they have a facecard you will lose.
Most players may bail on a potential flush if they only have 1 card in their hand, get 2 on the flop and need both the turn and river to be of that same suit. If, however, the flop itself has 3 of the same suit there are likely to be other players holding a spade who stayed in the game hoping on a fifth spade.
The above sort of thinking is also true with a straight. If you have an outside straight and your card is to the low side there is a good chance a competing player has an outside straight with a higher top card than you do.
The same sort of thinking is true if you flop a 3 of a kind where 2 of the pair are on the flop. Someone else playing may have the 4th of that card & they might also have a higher high card than you do or a full house with a higher second card. If you flop a 3 of a kind with all 3 being on the flop there is a good chance someone else will have a 4 of a kind or a full house with another pair.
Like This Game? Review This Online Virtual Texas Hold Em Poker Game
Banana Poker Card Game Play & Rules Screenshots




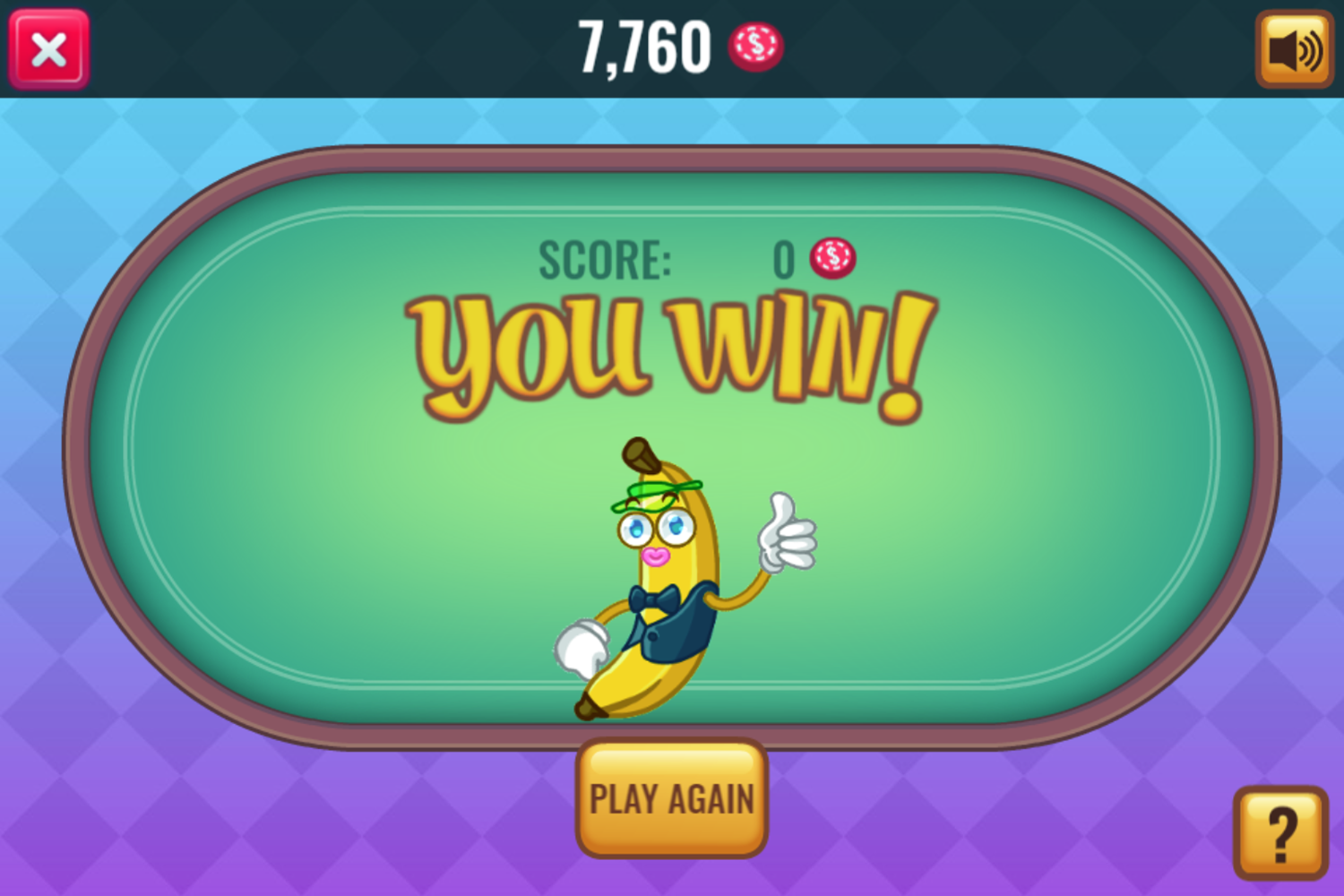
Mobile Friendly Cross Browser Support
This game is rendered in mobile-friendly HTML5, so it offers cross-device gameplay. You can play it on mobile devices like Apple iPhones, Google Android powered cell phones from manufactures like Samsung, tablets like the iPad or Kindle Fire, laptops, and Windows-powered desktop computers. All game files are stored locally in your web browser cache. This game works in Apple Safari, Google Chrome, Microsoft Edge, Mozilla Firefox, Opera and other modern web browsers.
Where To? What Next?
This game was published in these categories: Poker. You can visit any of them to select other fun games to play.
Our site hosts thousands of free online games. Check out the newest additions to our library or play a random game!
This game was published using our teamwide CardGames.pro account. If you have any comments, questions, concerns, or others (are there others even???) you can use the comments below to send along your 2 cents and help us improve the site further :) Your 2 cents plus 3 cents will buy you a nickel, but if your comments are genuinely useful and/or helpful and/or funny and/or memorable in a good way, we will probably say thanks :D
Search And Find And CardGames.pro Your Free Online Games :)










